Behzad Tabibian

Behzad Tabibian

I am a PhD student at Max Planck Institute - Intelligent Systems, working with Manuel Gomez-Rodriguez and Bernhard Schölkopf. I am interested in Machine Learning and Social Netwroks.

02-Integer-Linear-Programming

8 minute read

In [1]:

1
2
3
4
5
6
7

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from IPython.display import display
import mlabwrap
import pulp
mlab=mlabwrap.init('/Applications/MATLAB_R2013a.app/bin/matlab')

Found version: 2013a at /Applications/MATLAB_R2013a.app/bin/matlab

                            < M A T L A B (R) >
                  Copyright 1984-2013 The MathWorks, Inc.
                     R2013a (8.1.0.604) 64-bit (maci64)
                             February 15, 2013


To get started, type one of these: helpwin, helpdesk, or demo.
For product information, visit www.mathworks.com.

>>

Introduction to Optimization

Homework 2

Seyed Behzad Tabibian

Question 1

\[\begin{align} \text{Max } 4x_1 + 3x_2+3x_3\\ \text{Subject to}:\\ 4x_1+2x_2+x_3\leq 10 \\ 3x_1+4x_2+2x_3\leq 14 \\ 2x_1+x_2+3x_3\leq 7 \\ x_1,x_2,x_3\geq 0\\ x_1,x_2,x_3 \in Z \end{align}\]

In [3]:

1
2
3
4
5
6

f=np.array([-4,-3,-3])
W=np.array([[4,2,1],[3,4,2],[2,1,3],[-1,0,0],[0,-1,0],[0,0,-1]])
B=np.array([10,14,7,0,0,0])
res= mlab.linprog(f,W,B)
print res
print 'z: ', -1*f.dot(res)

[ 1.2         2.20000001  0.79999999]
z:  13.7999999864

Picking $x_1 \leq 1$:

\[\begin{align} \text{Max } 4x_1 + 3x_2+3x_3\\ \text{Subject to}:\\ 4x_1+2x_2+x_3\leq 10 \\ 3x_1+4x_2+2x_3\leq 14 \\ 2x_1+x_2+3x_3\leq 7 \\ x_1 \leq 1 \\ x_1,x_2,x_3\geq 0\\ x_1,x_2,x_3 \in Z \end{align}\]

In [5]:

1
2
3
4
5
6
7

f=np.array([-4,-3,-3])
W_temp_1=np.concatenate((W, np.array([[1,0,0]])))
B_temp_1=np.concatenate((B, np.array([1])),axis=-1)
res=mlab.linprog(f,W_temp_1,B_temp_1)
res_temp=-1*f.dot(res)
print res
print 'z: ',res_temp

[ 1.          2.29999999  0.90000001]
z:  13.5999999665

Picking $x_1 \geq 2$:

\[\begin{align} \text{Max } 4x_1 + 3x_2+3x_3\\ \text{Subject to}:\\ 4x_1+2x_2+x_3\leq 10 \\ 3x_1+4x_2+2x_3\leq 14 \\ 2x_1+x_2+3x_3\leq 7 \\ x_1 \geq 2 \\ x_1,x_2,x_3\geq 0\\ x_1,x_2,x_3 \in Z \end{align}\]

In [7]:

1
2
3
4
5
6
7

f=np.array([-4,-3,-3])
W_temp_2=np.concatenate((W, np.array([[-1,0,0]])))
B_temp_2=np.concatenate((B, np.array([-2])),axis=-1)
res=mlab.linprog(f,W_temp_2,B_temp_2)
res_temp=-1*f.dot(res)
print res
print 'z: ',res_temp

[ 2.          0.59999998  0.80000001]
z:  12.1999999723

Therefore Picking $x_1 \leq 1$ yields higher objective function.

In [8]:

1
2

W=W_temp_1
B=B_temp_1

Picking $x_2 \leq 2$:

\begin{align} \text{Max } 4x_1 + 3x_2+3x_3
\text{Subject to}:
4x_1+2x_2+x_3\leq 10
3x_1+4x_2+2x_3\leq 14
2x_1+x_2+3x_3\leq 7
x_2 \leq 2
x_1 \leq 1
x_1,x_2,x_3\geq 0
x_1,x_2,x_3 \in Z \end{align}

In [9]:

1
2
3
4
5
6
7

f=np.array([-4,-3,-3])
W_temp_1=np.concatenate((W, np.array([[0,1,0]])))
B_temp_1=np.concatenate((B, np.array([2])),axis=-1)
res=mlab.linprog(f,W_temp_1,B_temp_1)
res_temp=-1*f.dot(res)
print res
print 'z: ',res_temp

[ 1.  2.  1.]
z:  13.0000000002

Picking $x_2 \geq 3$:

\[\begin{align} \text{Max } 4x_1 + 3x_2+3x_3\\ \text{Subject to}:\\ 4x_1+2x_2+x_3\leq 10 \\ 3x_1+4x_2+2x_3\leq 14 \\ 2x_1+x_2+3x_3\leq 7 \\ x_2 \geq 3 \\ x_1 \leq 1 \\ x_1,x_2,x_3\geq 0\\ x_1,x_2,x_3 \in Z \end{align}\]

In [11]:

1
2
3
4
5
6
7

f=np.array([-4,-3,-3])
W_temp_2=np.concatenate((W, np.array([[0,-1,0]])))
B_temp_2=np.concatenate((B, np.array([-3])),axis=-1)
res=mlab.linprog(f,W_temp_2,B_temp_2)
res_temp=f.dot(res)
print res
print 'z: ',-1*res_temp

[ -3.80282472e-11   3.00000000e+00   1.00000000e+00]
z:  12.0000000027

Picking first branch:

\[\begin{align} \text{Max } 4x_1 + 3x_2+3x_3\\ \text{Subject to}:\\ 4x_1+2x_2+x_3\leq 10 \\ 3x_1+4x_2+2x_3\leq 14 \\ 2x_1+x_2+3x_3\leq 7 \\ x_2 \leq 2 \\ x_1 \leq 1 \\ x_1,x_2,x_3\geq 0\\ x_1,x_2,x_3 \in Z \end{align}\]

Question 2

In [13]:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#initialise the model
for i in [0,1]:
    if i==0 :
        print 'Linear Programming'
    else:
        print 'Integer Linear Programming'
    model = pulp.LpProblem('Question 2', pulp.LpMaximize)
    # make a list of ingredients
    var_set = ['x_1', 'x_2', 'x_3']
    # create a dictionary of pulp variables with keys from ingredients
    # the default lower bound is -inf

    x = pulp.LpVariable.dict('%s', var_set, lowBound =0, cat=pulp.LpInteger if i else pulp.LpContinuous)
    cost = dict(zip(var_set, [4,3, 3]))
    model += sum( [cost[i] * x[i] for i in var_set])
    c_1={'x_1':4,
         'x_2':2,
         'x_3':1}
    c_2={'x_1':3,
         'x_2':4,
         'x_3':2}
    c_3={'x_1':2,
         'x_2':1,
         'x_3':3}
    model += sum([c_1[i]*x[i] for i in var_set]) <= 10.0
    model += sum([c_2[i]*x[i] for i in var_set]) <= 14.0
    model += sum([c_3[i]*x[i] for i in var_set]) <= 7.0

    %timeit model.solve()
    for i in var_set:
        print '%s: %s'%(i,x[i].value())

Linear Programming
100 loops, best of 3: 10.2 ms per loop
x_1: 1.2
x_2: 2.2
x_3: 0.8
Integer Linear Programming
100 loops, best of 3: 14.7 ms per loop
x_1: 1.0
x_2: 2.0
x_3: 1.0

Question 3

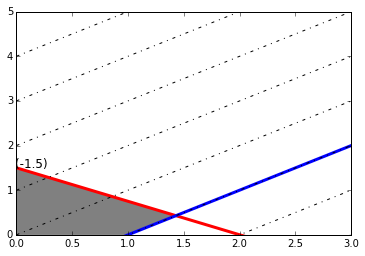
\[\begin{align} \text{Min } x - y\\ \text{Subject to}:\\ 3x+4y \leq 6 \\ x-y \leq 1 \\ x,y \geq 0\\ x,y \in Z \end{align}\]

In [15]:

1
2
3
4
5
6
7
8
9
10
11
12

x=np.arange(0,10)
c_1=-3.0/4*x+3.0/2
c_2=x-1
f=lambda b:(x+b)
plt.plot(c_1,'r',linewidth=3)
plt.plot(c_2,'b',linewidth=3)
feasible=np.array([[0,0],[0,1.5],[10.0/7,3.0/7],[1.0,0]])
plt.gca().add_patch(plt.Polygon(feasible,color='gray'))
map(lambda b:plt.plot(f(b),'-.k'),xrange(-3,9))
plt.text(0,1.5,'(-1.5)',fontsize=12)
plt.xlim(0,3)
_=plt.ylim(0,5)

png

In [16]:

1
2
3
4
5
6

f=np.array([1,-1])
W=np.array([[3,4],[1,-1],[-1,0],[0,-1]])
B=np.array([6,1,0,0])
res= mlab.linprog(f,W,B)
print res
print 'z: ', f.dot(res)

[ -6.37783160e-11   1.50000000e+00]
z:  -1.50000000011

In [17]:

1
2

A=np.array([[3,4,1,0,0,6],[1,-1,0,1,0,1],[1,-1,0,0,1,0]])
pd.DataFrame(A,index=['s_1','s_2','P'],columns=['x','y','s_1','s_2','P','b'])
x y s_1 s_2 P b
s_1 3 4 1 0 0 6
s_2 1 -1 0 1 0 1
P 1 -1 0 0 1 0

3 rows × 6 columns

\(\begin{align} y&=\frac{3}{2}-\frac{3}{4}x-\frac{1}{4}s_1=1.5\\ &=(1+\frac{1}{2})-(0+\frac{3}{4}x)-(0+\frac{1}{4}s_1)\\ &=(1)+(\frac{1}{2}-\frac{3}{4}x-\frac{1}{4}s_1)\\ \end{align}\) thus: \(\begin{align} \frac{1}{2}-\frac{3}{4}x-\frac{1}{4}s_1\leq 0\\ \end{align}\)

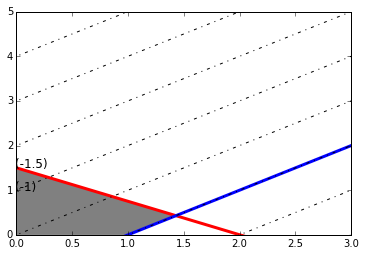
\[\begin{align} \text{Min } x - y\\ \text{Subject to}:\\ 3x+4y+s_1 = 6 \\ x-y \leq 1 \\ -\frac{3}{4}x-\frac{1}{4}s_1\leq -\frac{1}{2}\\ x,y \geq 0\\ x,y \in Z \end{align}\]

In [19]:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

x=np.arange(-3,10,0.5)
c_1=-1*(0.75)*x+3.0/2
c_2=x-1

#print c_3
f=lambda b:(x+b)
plt.plot(x,c_1,'r',linewidth=3)
plt.plot(x,c_2,'b',linewidth=3)

feasible=np.array([[0,0],[0,1.5],[10.0/7,3.0/7],[1.0,0]])
plt.gca().add_patch(plt.Polygon(feasible,color='gray'))
map(lambda b:plt.plot(x,f(b),'-.k'),xrange(-3,9))
plt.text(0,1.5,'(-1.5)',fontsize=12)
plt.text(0,1,'(-1)',fontsize=12)
plt.xlim(0,3)
_=plt.ylim(0,5)

png

In [20]:

1
2
3
4
5
6
7
8
9

f=np.array([1,-1,0])
W=np.array([[1,-1,0],[-3.0/4,0,-1.0/4],[-1,0,0],[0,-1,0],[0,0,-1]])
B=np.array([1,-1.0/2,0,0,0])
W_eq=np.array([[3,4,1]])
B_eq=np.array([6])

res= mlab.linprog(f,W,B,W_eq,B_eq)
print res
print 'z: ', f.dot(res)

[  2.95855784e-10   1.00000000e+00   2.00000000e+00]
z:  -0.999999999679

In [22]:

1
2

A=np.array([[3,4,1,0,0,0,6],[1,-1,0,1,0,0,1],[-3.0/4,0,-1.0/4,0,1,0,-1.0/2],[-1,1,0,0,0,1,0]])
pd.DataFrame(A,index=['s_1','s_2','t_1','P'],columns=['x','y','s_1','s_2','t','P','b'])
x y s_1 s_2 t P b
s_1 3.00 4 1.00 0 0 0 6.0
s_2 1.00 -1 0.00 1 0 0 1.0
t_1 -0.75 0 -0.25 0 1 0 -0.5
P -1.00 1 0.00 0 0 1 0.0

4 rows × 7 columns

Question 4

\[\begin{align} \text{Max } 4x_1+3x_2+x_3\\ \text{Subject to}:\\ 4x_1+2x_2+x_3 \leq 10 \\ 3x_1+4x_2+2x_3 \leq 14 \\ 2x_1+x_2+3x_3 \leq 7 \\ x_i \geq 0\\ x_i \in Z \end{align}\]

In [23]:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

model = pulp.LpProblem('Question 4', pulp.LpMaximize)
# make a list of ingredients
var_set = ['x_1', 'x_2','x_3']
# create a dictionary of pulp variables with keys from ingredients
# the default lower bound is -inf

x = pulp.LpVariable.dict('%s', var_set, lowBound =0, cat=pulp.LpInteger)
cost = dict(zip(var_set, [4,3,1]))
model += sum( [cost[i] * x[i] for i in var_set])
c_1={'x_1':4,
     'x_2':2,
     'x_3':1}
c_2={'x_1':3,
     'x_2':4,
     'x_3':2}
c_3={'x_1':2,
     'x_2':1,
     'x_3':3}
model += sum([c_1[i]*x[i] for i in var_set]) <= 10
model += sum([c_2[i]*x[i] for i in var_set]) <= 14
model += sum([c_3[i]*x[i] for i in var_set]) <= 7
print model
model.solve()
for i in var_set:
    print '%s: %s'%(i,x[i].value())
vals=np.array([float(x[i].value()) for i in var_set])
np.dot([4,3,3],vals)

Question 4:
MAXIMIZE
4*x_1 + 3*x_2 + 1*x_3 + 0
SUBJECT TO
_C1: 4 x_1 + 2 x_2 + x_3 <= 10

_C2: 3 x_1 + 4 x_2 + 2 x_3 <= 14

_C3: 2 x_1 + x_2 + 3 x_3 <= 7

VARIABLES
0 <= x_1 Integer
0 <= x_2 Integer
0 <= x_3 Integer

x_1: 2.0
x_2: 1.0
x_3: 0.0





11.0

In [26]:

1
2
3
4
5
6
7
8
9
10

def do_row(A,R,C):
    def check(r):
        if r!=R:
            return True
        else:
            return False
    def row_op(r):
        A[r,:]+=-A[r,C]*A[R,:]/A[R,C]
    map(row_op,filter(check,xrange(A.shape[0])))
    A[R,:]=A[R,:]/A[R,C]

In [43]:

1
2
3
4
5
6

f=np.array([-4,-3,-1])
W=np.array([[4,2,1],[3,4,2],[2,1,3],[-1,0,0],[0,-1,0],[0,0,-1]])
B=np.array([10,14,7,0,0,0])
res= mlab.linprog(f,W,B)
print res
print 'z: ', f.dot(res)

[  1.20000000e+00   2.60000000e+00   1.71098691e-11]
z:  -12.6

In [31]:

1
2
3
4
5
6
7
8

A=np.array([[4,2,1,1,0,0,0,10],[3,4,2,0,1,0,0,14],[2,1,3,0,0,1,0,7],[-4,-3,-1,0,0,0,1,0]])*1.0

do_row(A,0,0)
do_row(A,1,1)

A[2,:]=A[2,:]/A[2,2]
#print 2*A[0,:]+2*A[1,:]+A[2,:]
pd.DataFrame(A,index=['s_1','s_2','s_3','P'],columns=['x_1','x_2','x_3','s_1','s_2','s_3','P','b'])
x_1 x_2 x_3 s_1 s_2 s_3 P b
s_1 1 0 0.0 0.4 -0.2 0.0 0 1.2
s_2 0 1 0.5 -0.3 0.4 0.0 0 2.6
s_3 0 0 1.0 -0.2 0.0 0.4 0 0.8
P 0 0 0.5 0.7 0.4 0.0 1 12.6

4 rows × 8 columns

\(\begin{align} x_1&=-\frac{56}{10}-2x_2-\frac{6}{10}s_2+\frac{4}{10}s_3\\ &=-5\frac{3}{5}-2x_2-\frac{3}{5}s_2+\frac{2}{5}s_3\\ &=1 +1 + \{\frac{1}{5}-\frac{2}{5}s_1-\frac{4}{5}s_2\}\\ \end{align}\) thus: \(\begin{align} \frac{1}{5}-\frac{2}{5}s_1-\frac{4}{5}s_2\leq 0\\ \end{align}\)

\[\begin{align} \text{Max } 4x_1+3x_2+x_3\\ \text{Subject to}:\\ 4x_1+2x_2+x_3 +s_1= 10 \\ 3x_1+4x_2+2x_3+s_2 = 14 \\ 2x_1+x_2+3x_3 \leq 7 \\ -\frac{2}{5}s_1-\frac{4}{5}s_2\leq -\frac{1}{5}\\ x_i \geq 0\\ x_i \in Z \end{align}\]

In [162]:

1
2
3
4
5
6
7
8
9
10
11

f=np.array([-4,-3,-1,0])
W=np.array([[3,4,2,0],[2,1,3,0],[-1,0,0,0],[0,-1,0,0],[0,0,-1,0],[0,0,0,-1],[0,-1.0/2,-1.0/4,-1.0/4]])
print W
B=np.array([14,7,0,0,0,0,-1.0/2])
print B
W_eq=np.array([[4,2,1,1]])
B_eq=np.array([10])

res= mlab.linprog(f,W,B,W_eq,B_eq)
print res
print 'z: ', f.dot(res)

[[ 3.    4.    2.    0.  ]
 [ 2.    1.    3.    0.  ]
 [-1.    0.    0.    0.  ]
 [ 0.   -1.    0.    0.  ]
 [ 0.    0.   -1.    0.  ]
 [ 0.    0.    0.   -1.  ]
 [ 0.   -0.5  -0.25 -0.25]]
[ 14.    7.    0.    0.    0.    0.   -0.5]
[  1.20000000e+00   2.60000000e+00   2.77191248e-09   1.82848225e-09]
z:  -12.5999999939

In [160]:

1
2

A=np.array([[4,2,1,1,0,0,0,0,10],[3,4,2,0,1,0,0,0,14],[2,1,3,0,0,1,0,0,7],[0,-1.0/2,-1.0/4,-1.0/4,0,0,1,0,-1.0/2],[-4,-3,-1,0,0,0,0,1,0]])
pd.DataFrame(A,index=['s_1','s_2','s_3','t_1','P'],columns=['x_1','x_2','x_3','s_1','s_2','s_3','t_1','P','b'])
x_1 x_2 x_3 s_1 s_2 s_3 t_1 P b
s_1 4 2.0 1.00 1.00 0 0 0 0 10.0
s_2 3 4.0 2.00 0.00 1 0 0 0 14.0
s_3 2 1.0 3.00 0.00 0 1 0 0 7.0
t_1 0 -0.5 -0.25 -0.25 0 0 1 0 -0.5
P -4 -3.0 -1.00 0.00 0 0 0 1 0.0

5 rows × 9 columns

\(\begin{align} x_2&=\frac{7}{2}-\frac{3}{4}x_1-\frac{1}{2}x_3-\frac{1}{4}s_2=1.2\\ &=(3+\frac{1}{2})-(0+\frac{3}{4}x_1)-(0+\frac{1}{2}x_3)-(0+\frac{1}{4}s_2)\\ &=(3)+(\frac{1}{2}-\frac{3}{4}x_1-\frac{1}{2}x_3-\frac{1}{4}s_2)\\\\ \end{align}\) thus: \(\begin{align} \frac{1}{2}-\frac{3}{4}x_1-\frac{1}{2}x_3-\frac{1}{4}s_2 \leq 0 \end{align}\)

\[\begin{align} \text{Max } 4x_1+3x_2+x_3\\ \text{Subject to}:\\ 4x_1+2x_2+x_3 \leq 10 \\ 3x_1+4x_2+2x_3 \leq 14 \\ 2x_1+x_2+3x_3 \leq 7 \\ -\frac{1}{2}x_2-\frac{1}{4}x_3-\frac{1}{4}s_1\leq -\frac{1}{2}\\ -\frac{3}{4}x_1-\frac{1}{2}x_3-\frac{1}{4}s_2 \leq -\frac{1}{2}\\ x_i \geq 0\\ x_i \in Z \end{align}\]

In [1]:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

f=np.array([-4,-3,-1,0,0])
W=np.array([[2,1,3,0,0],
            [-1,0,0,0,0],
            [0,-1,0,0,0],
            [0,0,-1,0,0],
            [0,0,0,-1,0],
            [0,0,0,0,-1],
            [0,-1.0/2,-1.0/4,-1.0/4,0],
            [-3.0/4,0,-1.0/2,0,-1.0/4]])
print W
B=np.array([7,0,0,0,0,-1.0/2,-1.0/2])
print B
W_eq=np.array([[4,2,1,1,0],[3,4,2,0,1]])
B_eq=np.array([10,14])

#res= mlab.linprog(f,W,B,W_eq,B_eq)
#print res
#print 'z: ', f.dot(res)

[[ 2.    1.    3.    0.    0.  ]
 [-1.    0.    0.    0.    0.  ]
 [ 0.   -1.    0.    0.    0.  ]
 [ 0.    0.   -1.    0.    0.  ]
 [ 0.    0.    0.   -1.    0.  ]
 [ 0.    0.    0.    0.   -1.  ]
 [ 0.   -0.5  -0.25 -0.25  0.  ]
 [-0.75  0.   -0.5   0.   -0.25]]
[ 7.   0.   0.   0.   0.  -0.5 -0.5]

Question 5

Decision variables:

\[\begin{align} \text{Max: } \sum_1^6 r_i p_i\\ \text{Subject to:}\\ \sum_1^6 c_{1i} p_i \leq 250\\ \sum_1^6 c_{2i} p_i \leq 75\\ \sum_1^6 c_{3i} p_i \leq 50\\ \sum_1^6 c_{4i} p_i \leq 50\\ \sum_1^6 c_{5i} p_i \leq 50\\ \end{align}\]

Where $r_i$ represents revenue for project $i$,$c_{ki}$ represents costs for project $i$ at year $k$ and $p_i=0/1$ represents whether project $i$ is selected.

In [5]:

1
2
3
4
5
6
7
8
9
10
11
12
13

R=np.array([141,187,121,83,262,127])
C=np.array([[75,25,20,15,10],
            [90,35,0,0,30],
            [60,15,15,15,15],
            [30,20,10,5,5],
            [100,25,20,20,20],
            [50,20,10,30,40],
            ])
W=C.T
B=np.array([250,75,50,50,50])
res= mlab.bintprog(-1*R,W,B)
print res
print 'z: ', R.dot(res)

[ 1.  0.  0.  1.  1.  0.]
z:  486.0

You May Also Enjoy

Latent Dirichlet Allocation

[\newcommand{\EE}{\mathbb{E}} \newcommand{\wb}{\mathbf{w}} \newcommand{\zb}{\mathbf{z}} \newcommand{\Poisson}{\text{Poisson}} \newcommand{\Dir}{\text{Dir}}...

Public shaming, Weapon of mass destruction

5 minute read

Internet is very dear to me! That may sound strange but I come from a generation where I understand the difference between Internet and no Internet. I can st...

Lecture 5

16 minute read

Sympy - Symbolic algebra in Python