Behzad Tabibian

Behzad Tabibian

I am a PhD student at Max Planck Institute - Intelligent Systems, working with Manuel Gomez-Rodriguez and Bernhard Schölkopf. I am interested in Machine Learning and Social Netwroks.

01-Simplex-Method

11 minute read

In [2]:

1
2
3
4
5
6

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from IPython.display import display
#import mlabwrap
#mlab=mlabwrap.init('/Applications/MATLAB_R2013a.app/bin/matlab')

Introduction to Linear Programming

Question 1 - A

\[\begin{align} \text{Max } P(x; y) = 5x + 2y\\ \text{Subject to}:\\ x + y \geq 2\\ 2x + y \geq 4\\ x; y \geq 0\\ \end{align}\]

In [112]:

1
2
3
4
5
6
7
8
9
10
11
12
13

x=np.arange(0,10)
c_1=-1*x+2
c_2=-2*x+4
f=lambda b:(-2.5*x+b)
plt.plot(c_1,'r',linewidth=3)
plt.plot(c_2,'b',linewidth=3)
feasible=np.array([[0,4],[0,5],[5,5],[5,0],[2,0]])
plt.gca().add_patch(plt.Polygon(feasible,color='gray'))
map(lambda b:plt.plot(f(b),'-.k'),xrange(0,9))
plt.text(2,0.2,'(10)',fontsize=12)
plt.text(0.1,4,'(8)',fontsize=12)
plt.xlim(0,3)
_=plt.ylim(0,5)

png

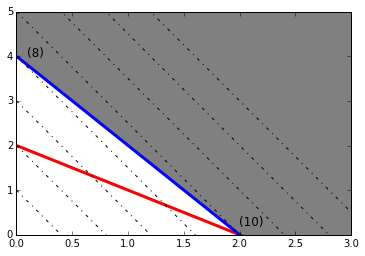
It is clear from the plot that the Maximization problem is unbounded and the solution to minimization problem is (0,4)

Matlab Linear Programming solution, which corresponds to infinity:

In [12]:

1
2
3
4

f=np.array([-5,-2])
W=np.array([[-1,-1],[-2,-1],[-1,0],[0,-1]])
B=np.array([-2,-4,0,0])
mlab.linprog(f,W,B)

array([  5.99065774e+21,   2.62912198e+05])

Question 1 - B

\[\begin{align} \text{Min } P(x; y) = 5x + 2y\\ \text{Subject to}:\\ x + y \geq 2\\ 2x + y \geq 4\\ x; y \geq 0\\ \end{align}\]

Matlab Linear Programming solution:

In [8]:

1
2
3
4

f=np.array([5,2])
W=np.array([[-1,-1],[-2,-1],[-1,0],[0,-1]])
B=np.array([-2,-4,0,0])
mlab.linprog(f,W,B)

array([  2.29759394e-08,   3.99999995e+00])

Which we solve by using the dual problem:

In [41]:

1
2
3

A=np.array([[1,1,2],[2,1,4],[5,2,1]])
print 'A=\n',A
print 'A\'=\n',A.T

A=
[[1 1 2]
 [2 1 4]
 [5 2 1]]
A'=
[[1 2 5]
 [1 1 2]
 [2 4 1]]

Which corresponds to following problem: \(\begin{align} \text{Max } P(x; y) = 2x + 4y\\ \text{Subject to}:\\ x + 2y \leq 5\\ x + y \leq 2\\ x; y \geq 0\\ \end{align}\)

Writing down the augumented matrix:

In [53]:

1
2

A=np.array([[1,2,1,0,0,5],[1,1,0,1,0,2],[-2,-4,0,0,1,0]])
pd.DataFrame(A,index=['s_1','s_2','P'],columns=['x','y','s_1','s_2','P','b'])
x y s_1 s_2 P b
s_1 1 2 1 0 0 5
s_2 1 1 0 1 0 2
P -2 -4 0 0 1 0

3 rows × 6 columns

Which has following basic solution: \(\begin{align} x=&0\\ y=&0\\ P=&0\\ s_1=&5\\ s_2=&2\\ \end{align}\)

choosing column $y$ as pivot column and row $s_2$ as pivot row we do the pivot operation:

In [54]:

1
2
3

A[0,:]=A[0,:]-2*A[1,:]
A[2,:]=A[2,:]+4*A[1,:]
pd.DataFrame(A,index=['s_1','y','P'],columns=['x','y','s_1','s_2','P','b'])
x y s_1 s_2 P b
s_1 -1 0 1 -2 0 1
y 1 1 0 1 0 2
P 2 0 0 4 1 8

3 rows × 6 columns

This is matrix provides us with the solution: \(\begin{align} x=s_1&=0\\ y=s_2&=4\\ \end{align}\)

Question 2

\[\begin{align} \text{Max } P(x; y) = 20x + 10y\\ \text{Subject to}:\\ x + y \geq 2\\ x + y \leq 8\\ 2x + y \leq 10\\ x; y \geq 0\\ \end{align}\]

In [16]:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

x=np.arange(0,11)
c_1=-1*x+2
c_2=-1*x+8
c_3=-2*x+10
f=lambda b:(-2*x+b/10.0)
plt.plot(c_1,'r',linewidth=3)
plt.plot(c_2,'b',linewidth=3)
plt.plot(c_3,'g',linewidth=3)
feasible=np.array([[0,2],[0,8],[2,6],[5,0],[2,0]])
plt.gca().add_patch(plt.Polygon(feasible,color='gray'))
map(lambda b:plt.plot(f(b),'-.k'),xrange(0,110,10))
plt.text(0,2.2,'(20)',fontsize=12)
plt.text(0,8,'(80)',fontsize=12)
plt.text(2,6,'(100)',fontsize=12,weight='bold')
plt.text(5,0.2,'(100)',fontsize=12,weight='bold')
plt.text(2,0.2,'(40)',fontsize=12)
plt.xlim(0,10)
_=plt.ylim(0,10)

png

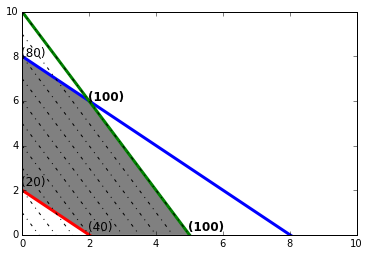
Matlab Linear Programming solution:

In [17]:

1
2
3
4

f=np.array([-20,-10])
W=np.array([[-1,-1],[1,1],[2,1],[-1,0],[0,-1]])
B=np.array([-2,8,10,0,0])
#mlab.linprog(f,W,B)

In [18]:

1
2

A=np.array([[1,1,-1,0,0,0,2],[1,1,0,1,0,0,8],[2,1,0,0,1,0,10],[20,10,0,0,0,1,0]])
pd.DataFrame(A,index=['s_1','s_2','s_3','P'],columns=['x','y','s_1','s_2','s_3','P','b'])
x y s_1 s_2 s_3 P b
s_1 1 1 -1 0 0 0 2
s_2 1 1 0 1 0 0 8
s_3 2 1 0 0 1 0 10
P 20 10 0 0 0 1 0

4 rows × 7 columns

\[\begin{align} x=&0\\ y=&0\\ P=&0\\ s_1=&-2\\ s_2=&8\\ s_3=&10 \end{align}\]

In [32]:

1
2
3

M=1000
A=np.array([[1,1,-1,0,0,1,0,2],[1,1,0,1,0,0,0,8],[2,1,0,0,1,0,0,10],[-20,-10,0,0,0,M,1,0]])
pd.DataFrame(A,index=['s_1','s_2','s_3','P'],columns=['x','y','s_1','s_2','s_3','a_1','P','b'])
x y s_1 s_2 s_3 a_1 P b
s_1 1 1 -1 0 0 1 0 2
s_2 1 1 0 1 0 0 0 8
s_3 2 1 0 0 1 0 0 10
P -20 -10 0 0 0 1000 1 0

4 rows × 8 columns

In [33]:

1
2

A[3,:]+=-M*A[0,:]
pd.DataFrame(A,index=['a_1','s_2','s_3','P'],columns=['x','y','s_1','s_2','s_3','a_1','P','b'])
x y s_1 s_2 s_3 a_1 P b
a_1 1 1 -1 0 0 1 0 2
s_2 1 1 0 1 0 0 0 8
s_3 2 1 0 0 1 0 0 10
P -1020 -1010 1000 0 0 0 1 -2000

4 rows × 8 columns

\[\begin{align} x=&0\\ y=&0\\ P=&0\\ s_1=&0\\ s_2=&8\\ s_3=&10\\ a_1=&2\\ \end{align}\]

Here we write a simple function to do the pivot operation:

In [25]:

1
2
3
4
5
6
7
8
9

def do_row(A,R,C):
    def check(r):
        if r!=R:
            return True
        else:
            return False
    def row_op(r):
        A[r,:]+=-A[r,C]*A[R,:]/A[R,C]
    map(row_op,filter(check,xrange(A.shape[0])))

In [34]:

1

A

array([[    1,     1,    -1,     0,     0,     1,     0,     2],
       [    1,     1,     0,     1,     0,     0,     0,     8],
       [    2,     1,     0,     0,     1,     0,     0,    10],
       [-1020, -1010,  1000,     0,     0,     0,     1, -2000]])

In [28]:

1
2
3
4

R=0
C=0
do_row(A,R,C)
pd.DataFrame(A,index=['x','s_2','s_3','P'],columns=['x','y','s_1','s_2','s_3','a_1','P','b'])
x y s_1 s_2 s_3 a_1 P b
x 1 1 -1 0 0 1 0 2
s_2 0 0 1 1 0 -1 0 6
s_3 0 -1 2 0 1 -2 0 6
P 0 10 -20 0 0 1020 1 40

4 rows × 8 columns

In [29]:

1
2
3
4

R=2
C=2
do_row(A,R,C)
pd.DataFrame(A,index=['x','s_2','s_1','P'],columns=['x','y','s_1','s_2','s_3','a_1','P','b'])
x y s_1 s_2 s_3 a_1 P b
x 1 0 0 0 0 0 0 5
s_2 0 0 0 1 -1 0 0 3
s_1 0 -1 2 0 1 -2 0 6
P 0 0 0 0 10 1000 1 100

4 rows × 8 columns

\[\begin{align} x=&5\\ y=&0\\ P=&100\\ s_1=&3\\ s_2=&3\\ s_3=&0\\ a_1=&0\\ \end{align}\]

Since one of the constraint lines is parallel to objective function the whole line segment is optimal. The other end of the line is picked by Matlab solver.

Question 3 - A

In [193]:

1
2
3
4
5
6
7
8
9

%%latex
\begin{align}
\text{Max } P(x; y) =& 20x + 10y\\
\text{Subject to}:&\\
2x + 3y \geq& 30\\
2x + y \leq& 26\\
-2x + 5y \leq& 34\\
x; y \geq& 0\\
\end{align}

\begin{align} \text{Max } P(x; y) =& 20x + 10y
\text{Subject to}:&
2x + 3y \geq& 30
2x + y \leq& 26
-2x + 5y \leq& 34
x; y \geq& 0
\end{align}

In [254]:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

x=np.arange(0,51)
c_1=-2.0/3*x+30/3
c_2=-2.0*x+26.0
c_3=2.0/5*x+34/5.0
f=lambda b:(-2*x+b/10.0)
plt.plot(c_1,'r',linewidth=3)
plt.plot(c_2,'b',linewidth=3)
plt.plot(c_3,'g',linewidth=3)
feasible=np.array([[3,8],[8,10],[12,2]])
plt.gca().add_patch(plt.Polygon(feasible,color='gray'))
map(lambda b:plt.plot(f(b),'-.k'),xrange(0,300,30))
plt.text(3,8.2,'(140)',fontsize=12)
plt.text(8,10,'(260)',fontsize=12,weight='bold')
plt.text(12,2.2,'(260)',fontsize=12,weight='bold')

plt.xlim(0,50)
_=plt.ylim(0,50)

png

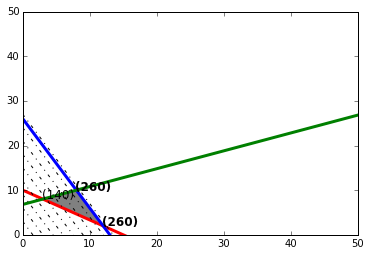
Matlab Linear Programming solution:

In [16]:

1
2
3
4

f=np.array([-20,-10])
W=np.array([[-2,-3],[2,1],[-2,5],[-1,0],[0,-1]])
B=np.array([-30,26,34,0,0])
mlab.linprog(f,W,B)

array([ 9.71445097,  6.57109806])

In [230]:

1
2

A=np.array([[2,3,-1,0,0,0,30],[2,1,0,1,0,0,26],[-2,5,0,0,1,0,34],[-20,-10,0,0,0,1,0]])
pd.DataFrame(A,index=['s_1','s_2','s_3','P'],columns=['x','y','s_1','s_2','s_3','P','b'])
x y s_1 s_2 s_3 P b
s_1 2 3 -1 0 0 0 30
s_2 2 1 0 1 0 0 26
s_3 -2 5 0 0 1 0 34
P -20 -10 0 0 0 1 0

4 rows × 7 columns

This is not a valid basic solution

\[\begin{align} \text{Max } P(x; y) =& 20x + 10y -Ma_1\\ \text{Subject to}:&\\ 2x + 3y -s_1+a_1=& 30\\ 2x + y \leq& 26\\ -2x + 5y \leq& 34\\ x; y \geq& 0\\ \end{align}\]

In [232]:

1
2

A=np.array([[2.0,3.0,-1.0,0,0,1.0,0,30.0],[2.0,1.0,0,1.0,0,0,0,26.0],[-2.0,5.0,0,0,1.0,0,0,34.0],[-20.0,-10,0,0,0,M,1.0,0]])
pd.DataFrame(A,index=['s_1','s_2','s_3','P'],columns=['x','y','s_1','s_2','s_3','a_1','P','b'])
x y s_1 s_2 s_3 a_1 P b
s_1 2 3 -1 0 0 1 0 30
s_2 2 1 0 1 0 0 0 26
s_3 -2 5 0 0 1 0 0 34
P -20 -10 0 0 0 1000 1 0

4 rows × 8 columns

In [233]:

1
2

A[3,:]+=-M*A[0,:]
pd.DataFrame(A,index=['a_1','s_2','s_3','P'],columns=['x','y','s_1','s_2','s_3','a_1','P','b'])
x y s_1 s_2 s_3 a_1 P b
a_1 2 3 -1 0 0 1 0 30
s_2 2 1 0 1 0 0 0 26
s_3 -2 5 0 0 1 0 0 34
P -2020 -3010 1000 0 0 0 1 -30000

4 rows × 8 columns

In [234]:

1
2
3
4

R=2
C=1
do_row(A,R,C)
pd.DataFrame(A,index=['a_1','s_2','y','P'],columns=['x','y','s_1','s_2','s_3','a_1','P','b'])
x y s_1 s_2 s_3 a_1 P b
a_1 3.2 0 -1 0 -0.6 1 0 9.6
s_2 2.4 0 0 1 -0.2 0 0 19.2
y -2.0 5 0 0 1.0 0 0 34.0
P -3224.0 0 1000 0 602.0 0 1 -9532.0

4 rows × 8 columns

In [235]:

1
2
3
4

R=0
C=0
do_row(A,R,C)
pd.DataFrame(A,index=['x','s_2','y','P'],columns=['x','y','s_1','s_2','s_3','a_1','P','b'])
x y s_1 s_2 s_3 a_1 P b
x 3.2 0 -1.000 0 -0.600 1.000 0 9.6
s_2 0.0 0 0.750 1 0.250 -0.750 0 12.0
y 0.0 5 -0.625 0 0.625 0.625 0 40.0
P 0.0 0 -7.500 0 -2.500 1007.500 1 140.0

4 rows × 8 columns

In [237]:

1
2
3
4

R=1
C=2
do_row(A,R,C)
pd.DataFrame(A,index=['x','s_1','y','P'],columns=['x','y','s_1','s_2','s_3','a_1','P','b'])
x y s_1 s_2 s_3 a_1 P b
x 3.2 0 0.00 1.333333 -2.666667e-01 0.00 0 25.6
s_1 0.0 0 0.75 1.000000 2.500000e-01 -0.75 0 12.0
y 0.0 5 0.00 0.833333 8.333333e-01 0.00 0 50.0
P 0.0 0 0.00 10.000000 1.132427e-13 1000.00 1 260.0

4 rows × 8 columns

\[\begin{align} x=&8.0\\ y=&10.0\\ P=&260\\ s_1=&16.0\\ s_2=&0\\ s_3=&0\\ a_1=&0\\ \end{align}\]

Question 3 - B

\[\begin{align} \text{Min } P(x; y) =& 20x + 10y\\ \text{Subject to}:&\\ 2x + 3y \geq& 30\\ 2x + y \leq& 26\\ -2x + 5y \leq& 34\\ x; y \geq& 0\\ \end{align}\]

Matlab Linear Programming solution:

In [17]:

1
2
3
4

f=np.array([20,10])
W=np.array([[-2,-3],[2,1],[-2,5],[-1,0],[0,-1]])
B=np.array([-30,26,34,0,0])
mlab.linprog(f,W,B)

array([ 3.,  8.])

This optimization problem is equal to:

\[\begin{align} \text{Max } P(x; y) =& -20x - 10y\\ \text{Subject to}:&\\ 2x + 3y \geq& 30\\ 2x + y \leq& 26\\ -2x + 5y \leq& 34\\ x; y \geq& 0\\ \end{align}\]

In [257]:

1
2

A=np.array([[2,3,-1,0,0,0,30],[2,1,0,1,0,0,26],[-2,5,0,0,1,0,34],[20,10,0,0,0,1,0]])
pd.DataFrame(A,index=['s_1','s_2','s_3','P'],columns=['x','y','s_1','s_2','s_3','P','b'])
x y s_1 s_2 s_3 P b
s_1 2 3 -1 0 0 0 30
s_2 2 1 0 1 0 0 26
s_3 -2 5 0 0 1 0 34
P 20 10 0 0 0 1 0

4 rows × 7 columns

\[\begin{align} \text{Max } P(x; y) =& -20x - 10y - Ma_1\\ \text{Subject to}:&\\ 2x + 3y -s_1+a_1=& 30\\ 2x + y \leq& 26\\ -2x + 5y \leq& 34\\ x; y \geq& 0\\ \end{align}\]

In [261]:

1
2

A=np.array([[2.0,3.0,-1.0,0,0,1.0,0,30.0],[2.0,1.0,0,1.0,0,0,0,26.0],[-2.0,5.0,0,0,1.0,0,0,34.0],[20.0,10,0,0,0,M,1.0,0]])
pd.DataFrame(A,index=['s_1','s_2','s_3','P'],columns=['x','y','s_1','s_2','s_3','a_1','P','b'])
x y s_1 s_2 s_3 a_1 P b
s_1 2 3 -1 0 0 1 0 30
s_2 2 1 0 1 0 0 0 26
s_3 -2 5 0 0 1 0 0 34
P 20 10 0 0 0 1000 1 0

4 rows × 8 columns

In [262]:

1
2

A[3,:]+=-M*A[0,:]
pd.DataFrame(A,index=['a_1','s_2','s_3','P'],columns=['x','y','s_1','s_2','s_3','a_1','P','b'])
x y s_1 s_2 s_3 a_1 P b
a_1 2 3 -1 0 0 1 0 30
s_2 2 1 0 1 0 0 0 26
s_3 -2 5 0 0 1 0 0 34
P -1980 -2990 1000 0 0 0 1 -30000

4 rows × 8 columns

In [263]:

1
2
3
4

R=2
C=1
do_row(A,R,C)
pd.DataFrame(A,index=['a_1','s_2','y','P'],columns=['x','y','s_1','s_2','s_3','a_1','P','b'])
x y s_1 s_2 s_3 a_1 P b
a_1 3.2 0 -1 0 -0.6 1 0 9.6
s_2 2.4 0 0 1 -0.2 0 0 19.2
y -2.0 5 0 0 1.0 0 0 34.0
P -3176.0 0 1000 0 598.0 0 1 -9668.0

4 rows × 8 columns

In [265]:

1
2
3
4

R=0
C=0
do_row(A,R,C)
pd.DataFrame(A,index=['x','s_2','y','P'],columns=['x','y','s_1','s_2','s_3','a_1','P','b'])
x y s_1 s_2 s_3 a_1 P b
x 3.2 0 -1.000 0 -0.600 1.000 0 9.6
s_2 0.0 0 0.750 1 0.250 -0.750 0 12.0
y 0.0 5 -0.625 0 0.625 0.625 0 40.0
P 0.0 0 7.500 0 2.500 992.500 1 -140.0

4 rows × 8 columns

\[\begin{align} x=&3.0\\ y=&8.0\\ P=&-140\\ s_1=&0\\ s_2=&12\\ s_3=&0\\ a_1=&0\\ \end{align}\]

Question 4

\[\begin{align} \text{Max } P(x; y) =& x+y\\ \text{Subject to}:&\\ 2x + y \leq 16\\ x \leq& 6\\ y \leq& 10\\ x; y \geq& 0\\ \end{align}\]

In [311]:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

x=np.arange(0,21)
y=np.arange(0,21)
c_1=-2.0*x+16
c_3=np.ones(51)*10
f=lambda b:(-1*x+b)
plt.plot(c_1,'r',linewidth=3)
plt.vlines(6,0,51,'b',linewidth=3)
plt.plot(c_3,'g',linewidth=3)
feasible=np.array([[0,0],[0,10],[3,10],[6,4],[6,0]])
plt.gca().add_patch(plt.Polygon(feasible,color='gray'))
map(lambda b:plt.plot(f(b),'-.k'),xrange(20))
plt.text(0.1,0.2,'(0)',fontsize=12)
plt.text(0,10.2,'(10)',fontsize=12)
plt.text(3,10.2,'(13)',fontsize=12,weight='bold')
plt.text(6.1,4.2,'(10)',fontsize=12)
plt.text(6,0,'(6)',fontsize=12)

plt.xlim(0,20)
_=plt.ylim(0,20)

png

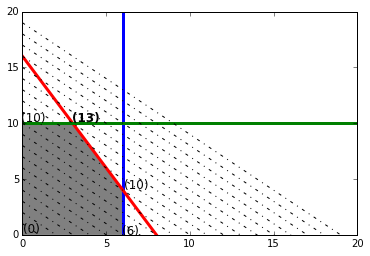
Matlab Linear Programming solution:

In [18]:

1
2
3
4

f=np.array([-1,-1])
W=np.array([[2,1],[1,0],[0,1],[-1,0],[0,-1]])
B=np.array([16,6,10,0,0])
mlab.linprog(f,W,B)

array([  3.,  10.])

In [277]:

1
2

A=np.array([[2,1,1,0,0,0,16],[1,0,0,1,0,0,6],[0,1,0,0,1,0,10],[-1,-1,0,0,0,1,0]])
pd.DataFrame(A,index=['s_1','s_2','s_3','P'],columns=['x','y','s_1','s_2','s_3','P','b'])
x y s_1 s_2 s_3 P b
s_1 2 1 1 0 0 0 16
s_2 1 0 0 1 0 0 6
s_3 0 1 0 0 1 0 10
P -1 -1 0 0 0 1 0

4 rows × 7 columns

We first pick column 1:

In [278]:

1
2
3
4

R=1
C=0
do_row(A,R,C)
pd.DataFrame(A,index=['s_1','x','s_3','P'],columns=['x','y','s_1','s_2','s_3','P','b'])
x y s_1 s_2 s_3 P b
s_1 0 1 1 -2 0 0 4
x 1 0 0 1 0 0 6
s_3 0 1 0 0 1 0 10
P 0 -1 0 1 0 1 6

4 rows × 7 columns

In [279]:

1
2
3
4

R=0
C=1
do_row(A,R,C)
pd.DataFrame(A,index=['y','x','s_3','P'],columns=['x','y','s_1','s_2','s_3','P','b'])
x y s_1 s_2 s_3 P b
y 0 1 1 -2 0 0 4
x 1 0 0 1 0 0 6
s_3 0 0 -1 2 1 0 6
P 0 0 1 -1 0 1 10

4 rows × 7 columns

In [280]:

1
2
3
4

R=2
C=3
do_row(A,R,C)
pd.DataFrame(A,index=['y','x','s_2','P'],columns=['x','y','s_1','s_2','s_3','P','b'])
x y s_1 s_2 s_3 P b
y 0 1 0 0 1 0 10
x 1 0 0 0 -1 0 3
s_2 0 0 -1 2 1 0 6
P 0 0 0 0 0 1 13

4 rows × 7 columns

\[\begin{align} x=&3.0\\ y=&10.0\\ P=&13\\ s_1=&0\\ s_2=&3\\ s_3=&0\\ \end{align}\]

In [284]:

1
2

A=np.array([[2,1,1,0,0,0,16],[1,0,0,1,0,0,6],[0,1,0,0,1,0,10],[-1,-1,0,0,0,1,0]])
pd.DataFrame(A,index=['s_1','s_2','s_3','P'],columns=['x','y','s_1','s_2','s_3','P','b'])
x y s_1 s_2 s_3 P b
s_1 2 1 1 0 0 0 16
s_2 1 0 0 1 0 0 6
s_3 0 1 0 0 1 0 10
P -1 -1 0 0 0 1 0

4 rows × 7 columns

Now we pick column 2:

In [285]:

1
2
3
4

R=2
C=1
do_row(A,R,C)
pd.DataFrame(A,index=['s_1','s_2','y','P'],columns=['x','y','s_1','s_2','s_3','P','b'])
x y s_1 s_2 s_3 P b
s_1 2 0 1 0 -1 0 6
s_2 1 0 0 1 0 0 6
y 0 1 0 0 1 0 10
P -1 0 0 0 1 1 10

4 rows × 7 columns

In [286]:

1
2
3
4

R=0
C=0
do_row(A,R,C)
pd.DataFrame(A,index=['x','s_2','y','P'],columns=['x','y','s_1','s_2','s_3','P','b'])
x y s_1 s_2 s_3 P b
x 2 0 1 0 -1 0 6
s_2 0 0 -1 1 0 0 3
y 0 1 0 0 1 0 10
P 0 0 0 0 0 1 13

4 rows × 7 columns

\[\begin{align} x=&3.0\\ y=&10.0\\ P=&13\\ s_1=&0\\ s_2=&3\\ s_3=&0\\ \end{align}\]

You May Also Enjoy

Latent Dirichlet Allocation

[\newcommand{\EE}{\mathbb{E}} \newcommand{\wb}{\mathbf{w}} \newcommand{\zb}{\mathbf{z}} \newcommand{\Poisson}{\text{Poisson}} \newcommand{\Dir}{\text{Dir}}...

Public shaming, Weapon of mass destruction

5 minute read

Internet is very dear to me! That may sound strange but I come from a generation where I understand the difference between Internet and no Internet. I can st...

Lecture 5

16 minute read

Sympy - Symbolic algebra in Python