01-Convex-Sets

In [1]:

import numpy as np
import matplotlib.pyplot as plt

This is the first notebook of the series going through Convex Optimizaion. The topics here are following MOOC Convex Optimization course by Stephen Boyd at Stanford.

In this notebook we will discuss preliminaries, mostly definitions used in later notebooks. This notebook covers some of the discussions in Chapter 2 of Convex Optimization book by Stephen Boyd.

---

Convex Sets

Affine set:

\[\begin{align} C \subseteq R^N\\ x_1,x_2 \in C, \theta \in R\\ \text{ then} \\ \theta x_1+(1-\theta)x_2 \in C\\ \end{align}\]

• If $C$ is affine set and $x_0 \in C$ we have:

  \[V=C-x_0=\{x-x_0 \mid x \in C\}\]

• Solution of a linear equation is an affine set.

• affine hull: The set of all affine combinations of points in some set $C \subseteq R^n$ and denoted aff $C$:

  aff $C= { \theta_1 x_1+\dots+\theta_k x_k \mid x_1,…x_k \in C,\theta_1+\dots+\theta_k = 1 }$

  if $S$ is any affine set with $C \subseteq S$, then aff $C \subseteq S$

In [2]:

plt.axis('equal')
C = np.array([[0,0],[0,2],[2,8],[3,9],[5,0],[4,1]])
C_1 = np.array([[2,8],[3,9]])
plt.xlim((-1,10))
plt.ylim((-1,10))
plt.grid()
plt.scatter(C[:,0],C[:,1],color='k',label='$C$')
region = plt.Rectangle((-20,-20),40,40,alpha=0.1,label='aff $C$')
plt.gca().add_patch(region)
plt.scatter(C_1[:,0],C_1[:,1],color='r',label='$C_1$')
plt.plot(np.arange(-10,10),np.arange(-10,10)* (C_1[0,1]-C_1[1,1])/(C_1[0,0]-C_1[1,0])+6,color='r',label='aff $C_1$')
plt.legend()

<matplotlib.legend.Legend at 0x10d0db910>

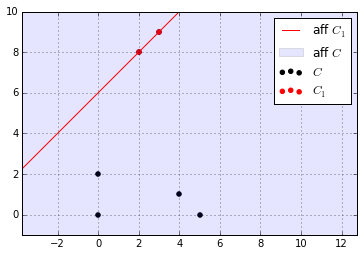
Affine dimension

• Affine dimension of a set is defined as dimension of its affine hull.
• If the affine dimension of a set $C \subseteq R^n$ is less than $n$, then $C$ lies in the affine set $\textbf{aff} C \neq R^n$.

Relative Interior

• relative interior of a set $C$:

  $\textbf{relint}={X \in C \mid B(x,r) \cap \textbf{aff} C \subseteq C, \text{for some} r > 0}$. note the $r>0$ condition excludes $x$ itself.

• relative boundary of a set $C$ is defined as : $\textbf{cl} C \setminus \textbf{relint} C$

---

Convex set

$\begin{align} C \subseteq R^N
x_1,x_2 \in C, \theta \in R \text{ and } 0 \leq \theta \leq 1\ \text{ then}
\theta x_1+(1-\theta)x_2 \in C
\end{align}$

• A set is convex if every point in the set can be seen by every other point, along an unobstructed straight line path between them.
• Every affine set is also convex.

• convex combination is a point of the form:

  $\theta_1 x_1 + \dots + x_k \theta_k$

  where $\theta_i \geq 0$ and $\theta_1 + \dots + \theta_k = 1$

Convex hull:

$ \textbf{Conv} C = \{ \theta_1 x_1 + \dots + \theta_k x_k \mid x_i \in C, \theta_i \geq 0, i=1,\dots,k, \theta_1+ \dots+\theta_k=1\}$

This can be generalized as:

Suppose $\theta_1, \theta_2, \dots$ satisfy:

$\theta_i\geq0, i=1,2,\dots, \sum_{i=1}^{\infty}\theta_i = 1$

and $x_1, x_2, \dots \in C$, where $C \subseteq R^n$ is convex. Then:

$\sum_{i=1}^{\infty}\theta_i x_i \in C$

If the series converges.

More generally suppose

$p: R^n \rightarrow R$ satisfies $p(x) \geq 0$ for all $x \in C$ and $\int_{C}p(x)dx=1$ where $C\subseteq R^n$ is convex, then

\[\int_{C}p(x)xdx \in C\]

if integral exist.

In [1]:

plt.axis('equal')
plt.xlim((-1,10))
plt.ylim((-1,10))
plt.grid()


C = np.array([[0,0],[0,2],[2,8],[3,9],[5,0],[4,1]])
plt.scatter(C[:,0],C[:,1],color = 'k',label = '$C$')
region=plt.Polygon([[0,0],[0,2],[4,1],[5,0]],alpha=0.1,label="conv $C$")
plt.gca().add_patch(region)

C_1 = np.array([[2,8],[3,9]])
plt.scatter(C_1[:,0],C_1[:,1],color = 'r',label = '$C_1$')
plt.plot(np.arange(2,4),np.arange(2,4)* (C_1[0,1]-C_1[1,1])/(C_1[0,0]-C_1[1,0])+6,color='r',label='conv $C_1$')


C_2 = [[1,4],[2,6.5],[3.5,5],[5,6],[5,4],[1,4]]
region=plt.Polygon(C_2,alpha = 0.1,color = 'r',label = "non convex set")
plt.gca().add_patch(region)
plt.legend()

<matplotlib.legend.Legend at 0x10b3ee150>

---

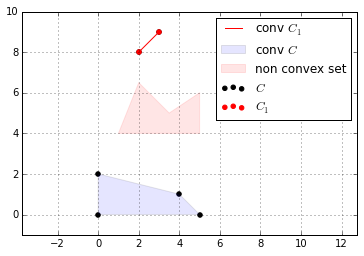
Cones

$\begin{align} C \subseteq R^N
\text{and}
x \in C, \theta \in R \text{ and } 0 \leq \theta \text{ then}
\theta x\in C
\end{align}$

• A set $C$ is convex cone if it is convex and cone:

  $\begin{align} x_1,x_2 \in C, \theta_1,\theta_2 \geq 0:
  \theta_1 x_1+\theta_2 x_2 \in C
  \end{align}$

• Points of this form form the two-dimensional pie slice with apex 0 and edges passing trhough $x_1$ and $x_2$.
• A set $C$ is a convex cone iff it contains all conic combinations of its elements.
• conic hull of a set $C$ is the set of all conic combinations of points in $C$: $\begin{align} \{\theta_1x_1+\dots+\theta_kx_k \mid x_i \in C, \theta_i \geq 0, i=1,\dots,k\} \end{align}$ Which is the smallest convex cone that contains $C$.

In [4]:

plt.axis('equal')
C = np.array([[0,0],[0,2],[2,8],[3,9],[5,0],[4,1]])
C_1 = np.array([[2,8],[3,9]])
plt.xlim((-1,10))
plt.ylim((-1,10))
plt.grid()
plt.scatter(C[:,0],C[:,1],color = 'k',label = '$C$')
region = plt.Polygon([[0,0],[0,20],[20,0]],alpha=0.1,label="con $C$")
plt.gca().add_patch(region)
plt.scatter(C_1[:,0],C_1[:,1],color = 'r',label = '$C_1$')
plt.legend()

<matplotlib.legend.Legend at 0x10d27b590>

---

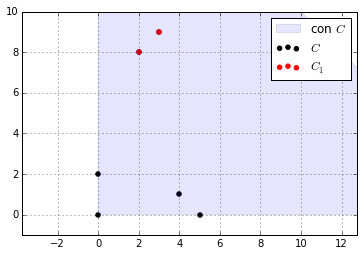
Examples

• The empty set $\emptyset$, any single point ${x_0}$, and the whole space $R^n$ are affine and thus convex subsets of $R^n$.
• Any line is affine. If it passes through zero, it is a subspace, hence a convex cone.
• A line segment is convex, but not affine.
• A ray, $\{x_0+\theta\nu \mid \theta\geq0\}$ where $\nu \neq 0$, is convex, but not affine. It is convex cone if its base is $x_0=0$.
• Any Subspace is affine, and a convex cone(hence convex)

• Halfspaces are convex:

  $C=\{x\mid a^Tx \leq b\}$

  if $x_0,x_1 \in C$ and $0 \leq \theta \leq 1$:

  $a^T(\theta x_0) + a^T((1-\theta)x_1) \leq \theta b + (1-\theta) b = b$

  and thus $(1-\theta)x_0+\theta x_1 \in C$

• A Euclidean ball: in $R^n$:

  \[B(x_c,r)=\{x \mid \parallel x-x_c \parallel_2 \leq r\} = \{x \mid (x-x_c)^T(x-x_c) \leq r^2\}\]

  is convex:

  \[\begin{align} \parallel \theta x_1 + (1-\theta)x_2 - x_c \parallel_2 &= \parallel \theta (x_1-x_c) - (1-\theta)(x_2 - x_c) \parallel_2\\ &\leq \theta \parallel (x_1-x_c) \parallel_2 + (1-\theta)\parallel (x_2 - x_c) \parallel_2 \text{Triangle inequality}\\ &\leq r \end{align}\]

• An Ellipsoid: in $R^n$:

  $\xi= {(x-x_c)^TP^{-1}(x-x_c)\leq 1}$

  where $P=P^T \succ 0$ (Symmetric and Positive definite).

  is convex.

In [5]:

from matplotlib.patches import Wedge
plt.axis('equal')
plt.grid()
region=plt.Circle([0,0],1,alpha = 0.1,label = "norm ball $R^2$")
plt.gca().add_patch(region)
w = Wedge([0,0], 0.5 , 0, 90,label = "euclidean norm con in $R^2$ $t=0.5$")
plt.gca().add_patch(w)
plt.plot([-1,1],[0,0],color='r',label = "norm ball $R$")
plt.xlim(-5,5)
plt.ylim(-5,5)
_=plt.legend()

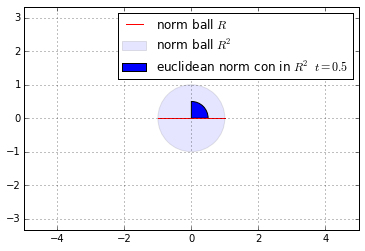
• A norm ball is any norm on $R^n$ .

  $B(x_c,r)=\{x\mid \parallel x-x_c \parallel \leq r\}$

  is convex.

• A norm cone associated with $\parallel \cdot \parallel$ is the set:

  $C=\{(x,t)\mid\parallel x \parallel \leq t\} \subseteq R^{n+1}$

  is convex cone.

In [8]:

import mpl_toolkits.mplot3d.axes3d as p3
fig=plt.figure()
ax = fig.gca(projection='3d')
x = np.arange(-5, 5, 0.1)
y = np.arange(-5, 5, 0.1)
xx, yy = np.meshgrid(x, y)
z = np.sqrt(xx**2+yy**2)
z[z>4] = np.nan
ax.plot_surface(xx,yy,z, rstride=1, cstride=1, cmap=cm.coolwarm,
        linewidth=0, antialiased=True)
_ = fig.suptitle('norm cone in $R^3$ with $r=4$', fontsize=14)

• Polyhedra is convex:

  $ P = \{x\mid a_j^T x \leq b_j, j= 1,\dots, m, c_j^Tx=d_j, j= 1,\dots,p\} = \{x \mid Ax\preceq b.Cx=d\}$

  • Simplexes are convex:

    Suppose the $k+1$ points $\nu_0,\dots,\nu_k \in R^n$ are affinely independent: $\nu_1-\nu_0,\dots,\nu_k-\nu_0$ are linearly independent. $C=conv\{\nu_0 , \dots , \nu_k\} = \{ \theta_0 \nu _0+\dots+\theta_k \nu_k \mid \theta \succeq 0,\boldsymbol{1}^T\theta=1\}$

    assume:

    \[\begin{align} x&=\theta_0\nu_0,\dots,\theta_k\nu_k\\ y&=(\theta_1,\dots,\theta_k)\\ B&=[\nu_1-\nu_0 \dots \nu_k-\nu_0]\in R^{n \times k}\\ \end{align}\]

    then

    \[\begin{align} x&=\nu_0+By\\ \end{align}\]

    We know that $B$ has rank $k$ thus there is a nonsingular matrix $A=(A_1,A_2)\in R^{n\times n}$ such that:

    \[\begin{align} AB= \begin{bmatrix} A_1\\ A_2 \end{bmatrix}B=\begin{bmatrix} I\\ 0 \end{bmatrix} \end{align}\]

    Multiplying \(x\) on the left with \(A\):

    \[\begin{align} A_1x=A_1\nu+y,A_2x=A_2\nu_0\\ \end{align}\]

    Which follows that:

    \[\begin{align} A\_2x&=A\_2\nu\_0 & & \\ A\_1x&\succeq A\_1\nu\_0& \text{ because } & y=A\_1x-A\_1\nu \succeq 0 \\ \boldsymbol{1}^TA\_1x&\leq\boldsymbol{1}^TA\_1\nu\_0& \text{ because }& \boldsymbol{1}^Ty\leq1 \\ &&&\boldsymbol{1}^T(A\_1x-A\_1\nu\_0)\leq 1\\ &&&\boldsymbol{1}^TA\_1x\leq 1+\boldsymbol{1}^TA\_1\nu\_0\\ \end{align}\]

    These are a set of linear equalities and inequalities and thus a polyhedra.

• Positive semidefinite cone:

  $ \boldsymbol{S}^n = \{X \in \boldsymbol{R}^{n\times n} \mid X=X^T \}$

  which is a vector space with dimension $n(n+1)/2$.

  $ \boldsymbol{S}^n_+ = \{X \in \boldsymbol{S}^{n} \mid X\succeq 0 \}$

  and

  $ \boldsymbol{S}^n_{++} = \{X \in \boldsymbol{S}^{n} \mid X\succ 0 \}$

  The set $\boldsymbol{S}^n_+$ is a convex cone: if: \(\begin{align} \theta_1,\theta_2\geq 0 A,B \in \boldsymbol{S}^n_+ \end{align}\) then: \(\begin{align} x^T(\theta_1A+\theta_2B)x=\theta_1x^TAx+\theta_2x^TBx\geq0 \end{align}\) The reason it is convex is discussed in next section.